Corso di Costruzioni per Istituti Tecnici indirizzo "Costruzioni Ambiente e Territorio"

Definizione

Le Travi Reticolari sono particolari travi costituite da un sistema di aste collegate alle estremità in punti detti nodi e hanno la peculiarità di essere soggette solo ad azione normale

Ipotesi di Lavoro "Travi Reticolari Isostatiche

Lo studio delle travi Reticolari prevede che:

1. Il sistema di aste deve costituire un sistema geometricamente indeformabile, trascurando le deformazioni elastiche delle aste. (in geometria l"unica figura che si può disegnare conoscendo solo la lunghezza dei lati è il triangolo, quindi le travi reticolari non sono altro che una seria di triangoli.)

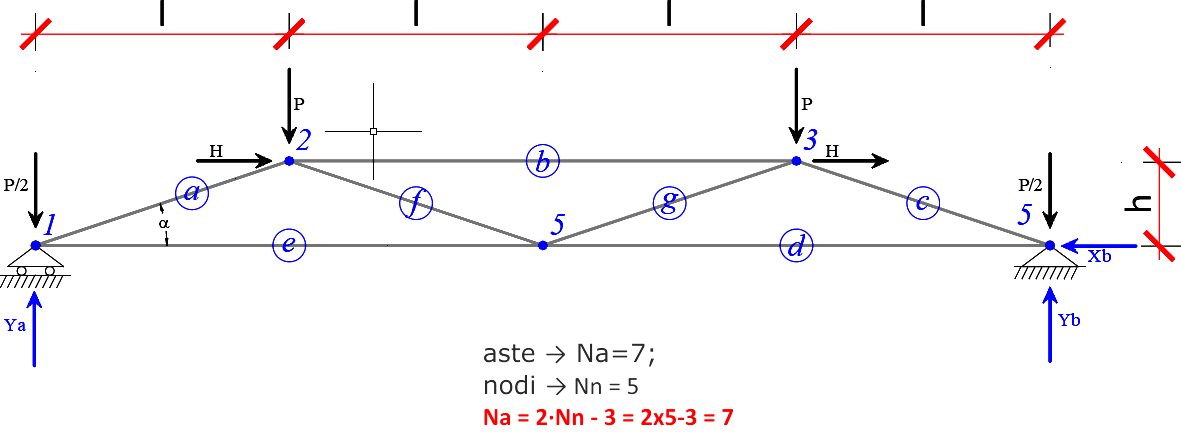
   questa condizione è espressa dall"equazione dei nodi che mette in relazione il numero delle aste con il numero dei nodi

   Equazione dei Nodi:

   N° aste = 2·n° nodi - 3

2. I carichi vanno applicati in corrispondenza dei nodi;
3. Nei nodi s"ipotizzano cerniere ideali

Le aste compresse sono chiamate "puntoni"

Le aste tesse sono chiamate "tiranti"

Isostaticità Travi Reticolari

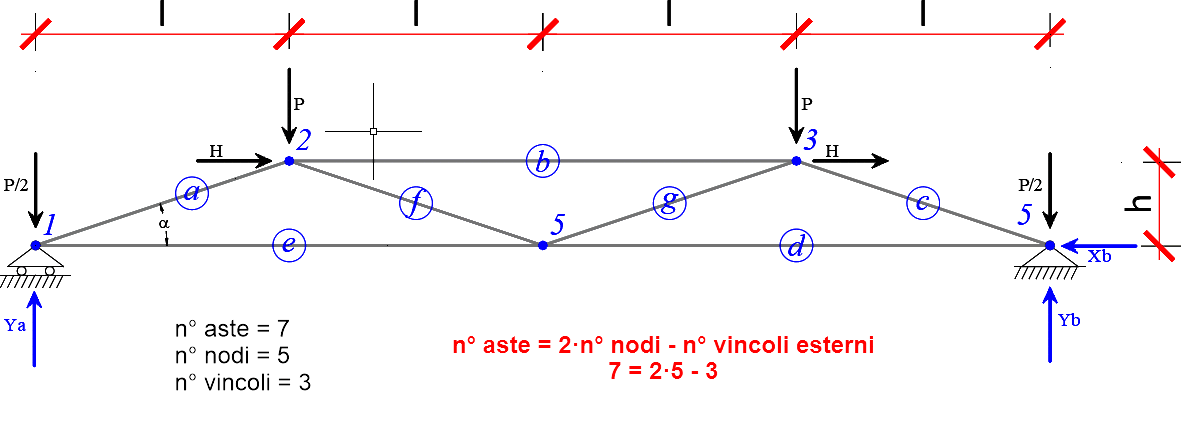
Ogni nodo (cerniera) ha nel piano due gradi di libertà, complessivamente l"intera struttura presenta 2·n°nodi gradi di libertà, sottraendo i vincoli esterni (n° vincoli ≥ 3), restano 2·n°nodi - n° vincoli gradi di libertà; poichè ogni asta (che si comporta come biella) è vincolo semplice, la condizione necessaria perchè la trave reticolare risulti isotatica risulta dalla seguente espressione:

n° aste = 2·n° nodi - n° vincoli esterni

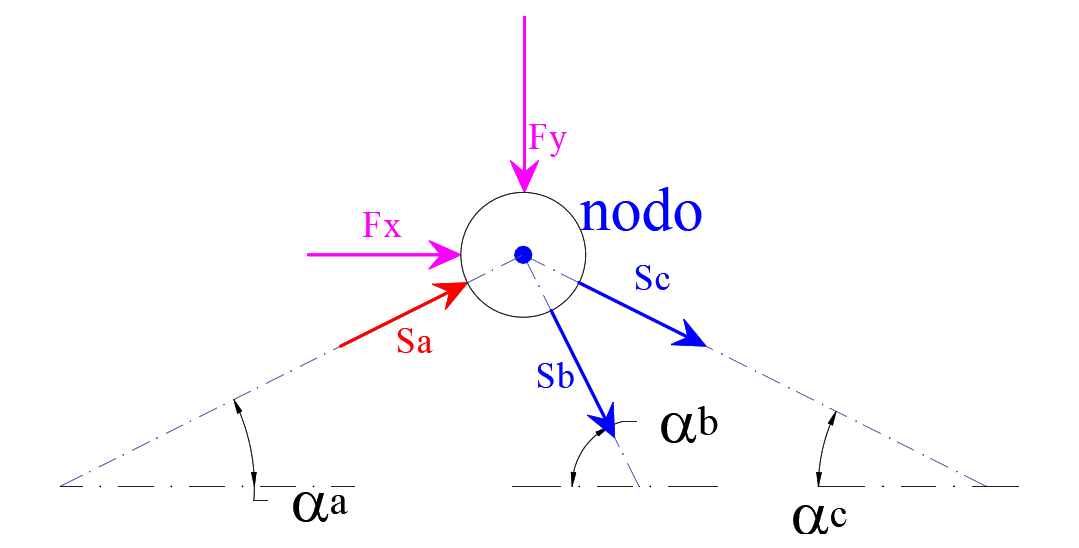
Calcolo degli sforzi metodo equilibrio ai nodi

Questo metodo consente di determinare l"entità degli sforzi nelle aste, procedendo, sequenzialmente, a partire dal nodo dove convergono non più di due aste (nodo Canonico), imponendo l"equilibrio alla traslazione orizzontale e verticale e risolvendo il sistema di equazioni.

Nell"esempio in fig. "2" Sa è noto perché è stato determinato in un nodo precedente, il suo verso è quello dello stato tensionale ricavato (puntone quando lo sforzo è diretto verso il nodo, tirante quando, invece, lo sforzo di allontana dal nodo)

Nella scrittura del sistema, si suggerisce, di prevedere gli sforzi incogniti come tiranti, pertanto se dal sistema il risulterà segno algebrico è positivo l"asta à un tirante, viceversa è un puntone.

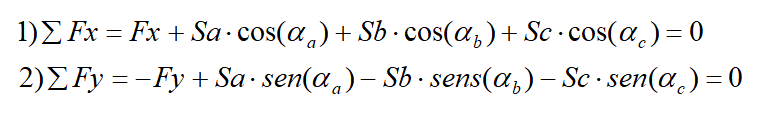
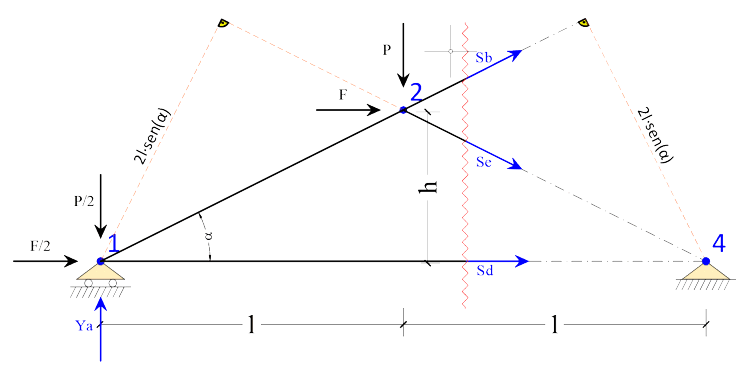
Calcolo degli sforzi metodo delle Sezioni Ritter

Questo metodo consente di determinare l"entità dello sforzo, in un"asta qualsiasi, imponendo che sia nullo l"equilibrio alla rotazione di tutte le forze che precedono (seguono) la sezione che tagli non più di tre aste (non convergenti tutte in uno stesso punto), rispetto al nodo dove convergono le aste tagliate che non sono oggetto del calcolo.

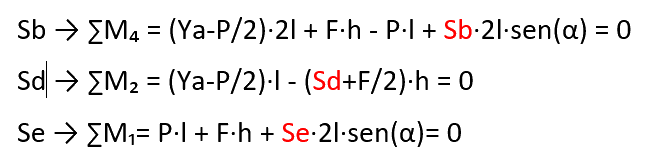
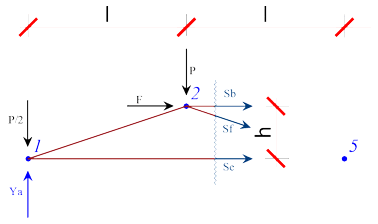
Se la trave presenta due correnti paralleli, per le aste di parete risulta impossibile applicare il metodo delle sezioni Ritter, per ottenere, comunque, una equazione con la sola incognita dello sforzo cercato, si impone l"equilibrio alla traslazione nella direzione perpendicolare ai correnti paralleli.

con riferimento alla fig. 5, per determinare gli sforzi nelle aste "h, e" parallele si applica le regole della sezioni Ritter.

per determinare lo sforzo nell"asta "f" con Ritter dovrei imporre l"equilibrio rispetto al punto di convergenza delle aste "h, e" che è inesistente essendo queste parallele; si impone, pertanto l"equilibrio alla traslazione orizzontale scrivendo un"equazione dove è presenta la sola incognita dello sforzo "Sf"

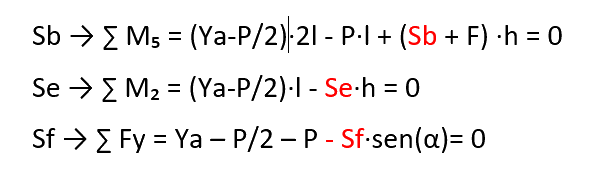
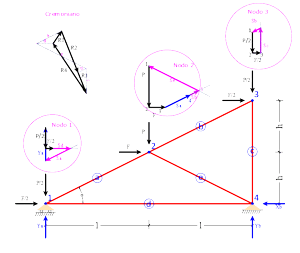
Calcolo degli sforzi metodo Grafico "diagramma reciproco o cremoniano"

Questo metodo è la costruzione grafica equivalente al metodo dell"equilibrio ai nodi. Si procede determinando:

1. le risultanti dei carichi esterni applicate ai singoli nodi (in figura R1, R2, ..., Rn)
2. a partire dal nodo dove convergono non più di due aste (in fig. il nodo 1), dagli estremi della risultante del carico esterno (R1) si riportano le direzione delle aste convergenti, ottenendo un triangolo. le lunghezze di questi lati indicano lo sforzo nelle rispettive aste (si ricorda che per l"equilibrio nel poligono delle forze i versi dei vettori si devono seguire quello della risultante esterna) mentre il verso da l"indicazione se l"asta è un puntone o un tirante.
3. si passa al nodo successivo, dove non siano presenti più di due aste incognite, lo sforzo determinato nel nodo precedente lo si considera con il verso opposto, quindi si tracciano le direzioni delle aste incognite ottenendo un poligono chiuso le cui lunghezze rappresentano li sforzi delle aste i versi seguono quello della risultante esterna.

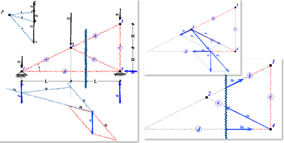
Calcolo degli sforzi metodo di Culmann

Il metodo di Culmanm permette di calcolare, attraverso un procedimento grafico, gli sforzi in tre aste concorrenti due a due in un punto, tagliate con una sezione che ha le stesse caratteristiche di quella di Ritter.

1.) Si determinata con la costruzione grafica del poligono funicolare la risultante R delle forze esterne (carichi sui nodi e reazione vincolare) che precedono la sezione.

2. si scompone la risultante ottenuta R, in tre componenti aventi rette di azione coincidenti con gli assi delle tre aste sezionate

3. per l’equilibrio gli sforzi nelle aste devono avere uguale intensità e verso contrario alle tre componenti; la scomposizione di una forza secondo tre componenti con direzione assegnata è possibile se le tre linee di azione si intersecano due a due.