Corso di Costruzioni per Istituti Tecnici indirizzo "Costruzioni Ambiente e Territorio"

1. m = massa:

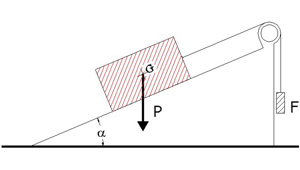
La MASSA è una grandezza fisica che esprime l’inerzia al moto di un corpo, cioè la sua attitudine ad opporsi a variazioni del proprio stato di quiete o di moto. Con riferimento alla fg. 01, un corpo di peso P, appoggiato su un piano inclinato, libero di muoversi in assenza di attrito e sul quale agiscono , non contemporaneamente le forze F1, F2, F3, ...,Fn, assume le accelerazioni a1, a2, a3, ...,an., sperimentalmente si osserva che

dove m è un coefficiente di proporzionalità chiamato massa del corpo ed è una costante che varia da corpo a corpo.

F → forza (N “Newton”)

m → massa (kg “chilogrammo”)

a → accelerazione (m/s² “metro su secondo quadro”

per i corpi soggetti all"azione gravitazionale la 2) diventa:

P → forza Peso (N “Newton”)

g → accelerazione di gravità (g=9.81....m/s²)

---

1. Peso specifico "è definito come il peso di un campione di materiale diviso per il suo volume"

γ → gamma (lettera greca) (N/m³)

P → Peso massa (N)

V → Volume (m^³)

1. Densità, (massa volumica o massa specifica) indica rapporto tra la massa di un corpo e il suo volume;

ρ → rho (lettera greca) (kg/m^³)

1. Sistema di masse

Un corpo può considerasi come un insieme di punti materiali di massa elementare detto sistema.

Sistema Discreto o Discontinuo

Si ha quando immaginiamo un corpo costituito da un numero finito di masse elementari

Sistema Continuo

Si ha quando immaginiamo un corpo costituito da un numero infinito di masse elementari adiacenti le une alle altre, tali da definire una entità geometrica (un segmento, una superficie, un volume)

Nello studio della geometria delle masse si considerano corpi omogenei, cioè che hanno le stesse caratteristiche fisico-chimiche in ogni punto, senza però definirene la loro natura.

Posto

la dimensione della massa coincide con le sue dimensioni geometriche, pertanto, un segmento può pensarsi come un sistema di masse lineari, una superficie come un sistema di masse superficiali e un volume come un sistema di masse volumiche.